Parábola Bloque IV

 

Construye mediante la parábola y sus elementos soluciones creativas a problemáticas del medio que lo rodea

Convierte de la ecuación ordinaria a la general, de manera crítica y reflexiva para representar y trazar parábolas presentes su contexto.

2.- Lugar geométrico de la parábola

2.1 Definición, elementos y trazado de la parábola

2.2 Ecuación de la parábola

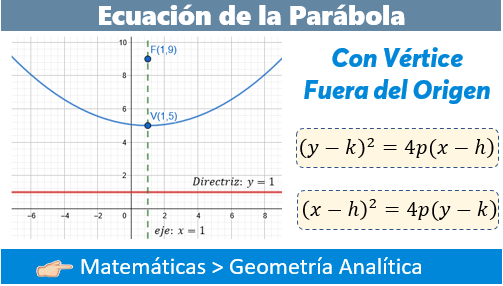
Ø  Ecuación ordinaria de parábolas verticales y horizontales con vértice en y fuera del origen

Ecuación general de la parábola

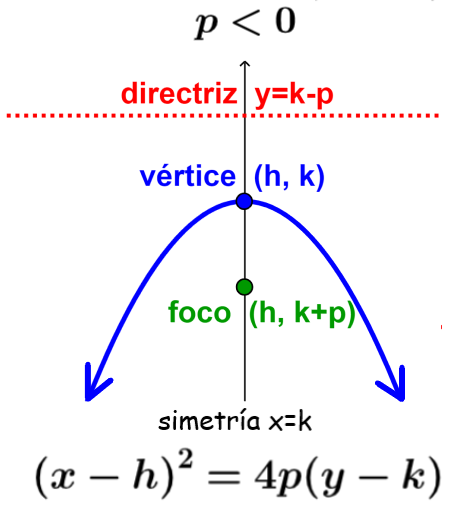
DEFINICIÓN DE PARÁBOLA

Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta llamada directriz.

El foco y la directriz determinan cómo va a ser la apariencia de la parábola (en el sentido de que “parecerá” más o menos abierta según sea la distancia entre F y la directriz).

Vértice: Es el punto medio entre el foco y la directriz.

Foco: Es el punto fijo F la parábola siempre abre hacia el foco

Directriz: Es la recta que pasa del lado contrario al foco y a la misma distancia

Distancia focal «p»: Es la distancia entre el vértice y el  foco

Eje: La recta perpendicular a la directriz y que pasa por el foco

Lado recto LR: es el ancho de la apertura de la parábola LR= /4p/

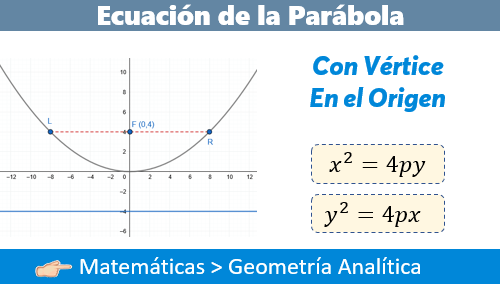
SE MUESTRAN LAS ECUACIONES DE LA PARABOLA CUANDO EL VERTICE COINCIDE CON EL ORIGEN

EJEMPLO: Obtener los elementos de la parábola dada su ecuación   y² = 20x   

La parábola será horizontal de acuerdo a su fórmula    y² = 4px

 y² = 20x    al compar la ecuación con el ejemlo observamos que 4p = 20

y² = 4px     por lo tanto tenemos que

4p = 20

Despejamos a p

p = 20/4

p = 5  es la distancia del vértice al foco 

EJEMPLO: obtener los elementos de la parábola dada su ecuación. x² = 16y   

La parábola será vertical según su fórmula    x² = 4py

Entonces comparamos

 x² = 16y   

x² = 4py       por lo tanto tenemos que

4p = 16

 Despejamos a p

p = 16/4

p = 4   es la distancia del centro al foco

SE MUESTRAN LAS ECUACIONES DE LA PARABOLA CUANDO EL VERTICE COINCIDE CON EL ORIGEN

Determina los elementos de la parábola a partir de la ecuación dada: